MATLAB implementation of an exact LWR solver Download

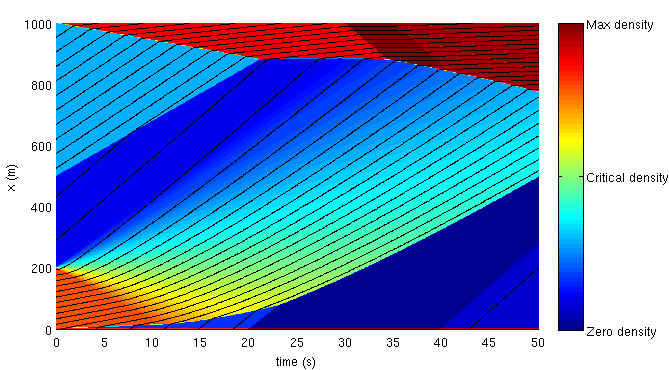
The Lighthill-Whitham-Richards Partial Differential Equation (LWR PDE) is a seminal equation in traffic flow theory. It leads to common yet widely used traffic flow models for highways. This package proposes a sample implementation for a LWR solver using a new Lax-Hopf method. In the literature, the LWR PDE is typically solved using the Cell Transmission Model (CTM), a Godunov scheme, which requires a grid to compute the solution numerically, and induces specific approximations of the solution (in addition to the errors of the numerical computation).

The proposed approach has the following features:

It is greed free: in order to compute the value at a given point x and a given time t, it is not necessary to grid space and time (only to prescribe initial and boundary data, and to enter the point where the solution should be computed).
It is exact: the program presented here computes the solution by evaluating a function numerically (rather than approximating derivatives of the PDE by finite differences).
It is has small computational cost: since it is not needed to grid the space, the computation is much faster than with finite difference methods (Godunov, CTM, etc.)

To get started:

Short manual (PDF) for the matlab package;
Article submitted to TR-B, analytical and grid-free solutions to the Lighthill-Whitham-Richards traffic flow model,
P.-E. Mazaré, C. Claudel, A. Bayen.
Article published on ScienceDirect.com, analytical and grid-free solutions to the Lighthill–Whitham–Richards traffic flow model, P.-E. Mazaré, A. Dehwah, C. Claudel, A. Bayen.

30-second how-to

script.m contains a sample script which creates a Lax-Hopf solver for a given Greenshields fundamental diagram and solves the Cauchy problem associated with an arbitrary set of initial densities, upstream and downstream flows;
two functions allow you to plot your results: LH_plot3D and LH_plot2D;
for advanced users, it is possible to solve the Cauchy problem associated with any concave fundamental diagram. Refer to the manual (PDF) for more details.

Important notes

The Matlab functions require Matlab version R2008A or newer. They may work under earlier Matlab versions, but have not been tested.
No additional toolboxes are required.
By downloading this software, you agree with the license terms.

References

More details about the foundations of this method can be found in the following publications:

Lax-Hopf based incorporation of internal boundary conditions into Hamilton-Jacobi equation. Part I: Theory, C. Claudel and A. Bayen. IEEE Transactions on Automatic Control 55(5) pp. 1142-1157, May 2010, doi: 10.1109/TAC.2010.2041976
Lax-Hopf based incorporation of internal boundary conditions into Hamilton-Jacobi equation. Part II: Computational methods, C. Claudel and A. Bayen. IEEE Transactions on Automatic Control 55(5) pp. 1158-1174, May 2010, doi: 10.1109/TAC.2010.2045439
Dirichlet problems for some Hamilton-Jacobi equations with inequality constraints, J.-P. Aubin, A. Bayen, P. Saint-Pierre, SIAM Journal on Control and Optimization, 47(5), pp. 2348ï¿½2380, 2008, doi:10.1137/060659569

Related work:

A variational formulation of kinematic waves: solution methods, C. Daganzo, Transportation Research Part B, 39(10), pp. 934-950, 2005
A variational formulation of kinematic waves: Bottleneck Properties and Examples, Daganzo, C.F. and M. Menendez , Proceedings, 16th International Symposium on Transportation and Traffic Theory (H. Mahmassani, editor) Elsevier, New York, N.Y., July 2005, pp.345-364.
On the numerical treatment of moving bottlenecks, C. Daganzo and J. Laval, Trans Res B 39(1), 31-46 (2005).